The Curious Cat
Superposition, tunnelling, entanglement, and other bits and pieces of quantum mechanics.

Superposition, tunnelling, entanglement, and other bits and pieces of quantum mechanics.
In Part 2, we discussed how the dual nature of the particle was discovered. We’ve also covered the “Uncertainty Principle”, why you can never know where a particle is for certain, and the “Measurement Problem” of why Now, I’ll try to explain most of the “quantum” phenomena that come out of that explanation.
For example: did you know that a particle can be in two places at once?
Let’s get back to the wave equation, and the “where the electron might be” graph. See the highest point over there? That’s called the “crest”, and it’s where the particle has the highest chance of being.
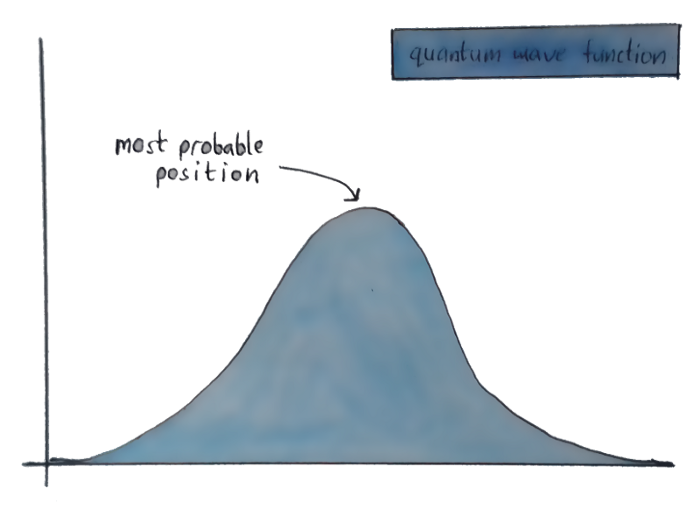
But suppose that the wave equation throws up a graph with two crests of equal amplitude? Then the particle is equally likely to be in both those places.

This might sound weird but is perfectly normal in the Quantum Realm. And this is where the phrase “Things can be at two places at once” comes from. In this world, we know that a particle can’t be present at two places at the same time, but we just aren’t sure where it exists. It can be at point A or at point B, but we can’t be sure of where it exactly is.
So if the electron has an equal probability of being at both points but not 100% at any, we say that it “exists ”at both the places. This is known as “Superposition”.
Erwin Schroedinger, one of the founding physicist of Quantum Mechanics, once did a thought experiment. I’m pretty sure, that you’ve heard some version of it.
In this, you put a cat in a bunker with unstable gunpowder that has a 50% chance of blowing up in the next minute, and an equal chance of not blowing up. Which means, that the cat has a high probability of surviving, but an equal probability of being killed.
Until we look inside, we don’t know whether the cat is alive or not. As far as we’re concerned, it’s in both the states — and our act of looking forces it to collapse into one, either dead or alive.

This is till date the most famous analogy for Superposition.
It’s not just where a particle is that can undergo superposition. “Superposition of state”, as its name suggests, is when an electron is both a particle and a wave at the same time, and becomes a particle once we observe it. But physicist like to call it a “particle-wave duality”.
State and position aren’t the only properties that particles have, though. Let me introduce you to a new concept: quantum numbers.
Quantum numbers are basically numbers that give us information about electrons orbiting a nucleus, just like bus numbers give us information about the route of a bus. They come out of Schroedinger’s equation, which we saw in Part 1. In the example of an electron, here’s what they tell us:
- The principal quantum number (N) is an integer that tells you at which position the electron is orbiting.
- The angular momentum quantum number (L) is an integer that is the value of the electron’s orbital. Remember what I told you, nothing is certain in the atomic world, so, we don’t know where the electron is and so we have marked specific areas around the nucleus, where the probability of finding the electron is most. This Quantum number gives us that “cloud” of probable places.
- The magnetic quantum number tells us the orientation of the orbital with respect of x, y, and the z plane
- The spin quantum number has two values “spin down” and “spin up”. An electron while revolving around the nucleus, rotates on its own axis just like the Earth. This quantum number tells us whether it’s spinning clockwise or anti-clockwise.
According to the Pauli exclusion principle, no two electrons in an atom can have the same set of quantum numbers. So if two electrons are in the same orbital, with the same orientation, then you can know for certain they’ll be spinning in opposite directions.
Let’s imagine two electron waves meet. When they do so, their peaks and troughs interfere with each other and get mixed up and eventually both the waves converge into a single wave. And because of this, we can describe both the electrons mathematically using just this one wave.
They are now inextricably linked, even if they move millions of miles away from each other. So measurement of one electron would tell us about the second one as well, even if they very far from one other.
Einstein was very uncomfortable with this idea cause, if you measure one particle here, you would instantaneously know all the information about the other, even if it’s billions of miles away. So there has to be some sort of instantaneous information transfer between the two. But if these two are light years apart, then for communication to happen instantaneously, signals must travel faster than light which is not possible if Einstein’s laws of Relativity are correct.
If Quantum particles can pass the barrier of time, you’d think a physical barrier would be no problem for them. Right?
You would, in fact, be right. It’s called “quantum tunneling”.

Let’s see this in terms of probability wave. When the wave meets the barrier, the probability wave’s amplitude reduces exponentially, but if the barrier is narrow enough, then the wave-function will still exist at the other side. That means that the electron has a decent probability of existing on the other side when a measurement is done.
So yeah, electrons can teleport through walls. Which is I think almost impossible to comprehend cause in our Newtonian minds and I’m pretty sure that by now you might be thinking of leaving this article. But, don’t worry we’re almost finished.
Quantum Tunnelling is actually the biggest challenge to modern computers. You might have seen new chipsets by Intel and Qualcomm, being made on seven-nanometer-small processors. But as they continue to shrink, the size of these chipsets, the size of physical transistors — the walls that block the flow of electrons — also shrink.
And that is the cause of worry because when the transistor is that small, electrons don’t stop. They quantum-tunnel through the wall, rendering the transistors and chips useless.
Luckily, that’s when Quantum Computing comes to our rescue, turning tunnelling, and superposition into an advantage. But that, I think, is a topic for our next instalment.
In quantum physics, objects are described using wave functions, but, when we measure them, they seem to act like particles. This is what leads to particle-wave duality and also the measurement problem. And because of these, we get weird things like Superposition, Quantum Tunnelling, Heisenberg’s Uncertainty Principle and energy quantization.
If you understood these, I think you got a basic understanding of what Quantum Mechanics really is, and I just made Big Bang Theory more fun for you.
Despite the typical prejudice, Quantum Mechanics is not that difficult to understand. Usually, people consider it difficult because it is very, very tough to imagine these strange mysterious events, that are so different from the world we see.
I think the weird part about Quantum Mechanics is, that on one side it has led to numerous discoveries and has really expanded our understanding of the universe tremendously, but on the other side, has many mysteries and holes like the measurement problem, that are just too strange for us to wrap our heads around.
I’m sure you must have encountered numerous confusions, but I’ll be happy to help you. Come, let’s discuss them below.
Quanta in a Nutshell: This article is third of a four-part series on quantum mechanics. Up next: superposition of bits, the entanglement of data, and how quantum computing may (and may not) change the world.
Want to write with us? To diversify our content, we’re looking out for new authors to write at Snipette. That means you! Aspiring writers: we’ll help you shape your piece. Established writers: Click here to get started.